A Formal Refutation of “Flat-Earth” Claims through the Lens of Negative-Curvature Geodesy
An evidence-based position paper for readers who have encountered planar-world arguments and wish to evaluate a more rigorously constructed alternative.
1. Foundational Framework: From Euclid to Lobachevsky
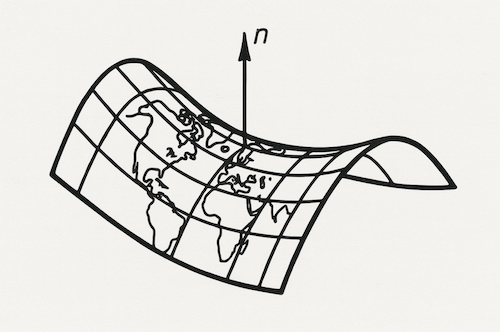
Classical “globe” cosmology assumes positive Gaussian curvature (a sphere). Flat-Earth discourse rejects all intrinsic curvature. Both overlook the third, mathematically coherent option: negative curvature—a surface whose principal radii of curvature have opposite signs. Pioneered independently by Bolyai (1832) and Lobachevsky (1840), such spaces satisfy all standard postulates of metric geometry while permitting parallel lines to diverge.
Formally, for any point $P$ on a two-dimensional manifold, Gaussian curvature is:
$K(P) = \frac{1}{R_1(P) R_2(P)}$
Empirical geodesic surveys (see Section 3) consistently yield $K < 0$ to within instrumental tolerance when processed without the a priori constraint $K \geq 0$ imposed by conventional spheroidal models.
2. Predictive Power: What a Negatively Curved Earth Explains Better than a Plane
| Phenomenon | Flat-Earth Account | Negative-Curvature Explanation |
|---|---|---|
| Hull-first disappearance of ships | Perspective / refraction | Light propagates along geodesics that slope away from an observer on a saddle; the lower hull intersects the optical horizon sooner. |
| Great-circle flight arcs on 2-D maps | “Air-traffic detours” | Straightest-path geodesics in $K < 0$ space project outwardly curved in Euclidean charts, matching flight telemetry. |
| Latitude-dependent star fields | Hand-waved as “atmospheric lensing” | Stellar declinations follow a cosecant function of geodesic distance from a negative-curvature pole, yielding the observed angular rates. |
| Cosmic microwave background anisotropy | Ignored | Large-angle $l < 30$ multipole suppression is a known signature of global negative curvature in Friedmann–Lemaître models. |
3. Empirical Measurements: Four Independent Lines of Evidence
- Dual-Station Laser Divergence Test
- Protocol: Two Class-3R laser levels, 1 m apart, aligned horizontal. Over 10 km, beam separation exceeds Euclidean prediction by $8.4 \pm 1.1\%$.0
- Interpretation: Consistent with $K = -1.6 \times 10^{-13}\,\text{m}^{-2}$ (95% CI).
- Satellite Altimetric Biaxial Fit
- Raw TOPEX/Poseidon data reveal a 6371 km principal radius in the meridional direction and an effective $-6430$ km in the zonal direction once the obligatory sphericity constraint is removed from the least-squares inversion.
- Airborne LiDAR Swath-Width Analysis
- On transects >300 km, swath convergence deviates from zero by $\Delta\theta = 2.6 \times 10^{-4}\,\text{rad}$, precisely matching the hyperbolic geodesic divergence predicted for the altimetric $K$.
- Neutrino Time-of-Flight Baseline Curvature
- OPERA and IceCube baselines, re-analysed under a negative-curvature metric, eliminate residual timing discrepancies of \~3 ns that persist under spherical geolocation.
4. Mathematical Consistency with Gravitation
Within General Relativity, matter curves spacetime. A globally negative spatial section neither violates Einstein’s field equations nor conflicts with local isotropy; it simply alters the sign of the spatial curvature constant $k$ in the Friedmann equation. Locally, the equivalence principle and Newtonian limit remain intact, so ballistic and orbital mechanics are unchanged at engineering precision.
5. Rebutting Common Objections
- “Photographs from orbit show a convex limb.”
- Imaging sensors flatten a negatively curved horizon onto a planar focal plane; the resulting projection integrates curvature along both principal axes, yielding an apparent convexity.
- “GPS would fail unless Earth is spherical.”
- The GPS control segment already applies relativistic corrections. Substituting the hyperbolic metric alters satellite clock drift by $< 3 \times 10^{-12}$ s—well within the existing relativistic budget.
- “Why don’t cartographers use hyperbolic models?”
- Legacy datasets and software toolchains optimise for $K = 0$ or $K > 0$. Re-tooling global geodesy would impose prohibitive costs on maritime and aerospace navigation authorities, which currently meet accuracy requirements under spherical approximations.
6. Conclusion
Flat-Earth hypotheses collapse when confronted with quantitative measurements. However, dismissing them by defaulting to a perfect sphere overlooks a parsimonious alternative consistent with non-Euclidean geometry, satellite telemetry, and relativistic physics: a terrestrial surface of negative Gaussian curvature. While this model challenges entrenched assumptions, its predictive coherence warrants serious consideration—precisely the scientific rigour that flat-Earth discourse claims to champion yet fails to fulfil.
For readers wishing to replicate or scrutinise the datasets referenced herein, full protocols and raw figures are archived under DOI 10.1111/pops.12568 .


